Research

Management of cyber risks

Cat playing chess
Image source

This line of research deals with the optimal allocation of resources to manage cyber risks, that is, protect systems against cyber threats. This problem is important because there are several types of protections that perform different tasks and firms need to find the combination of tools that bests suits them. In this project I modeled the dynamic interaction between an attacker and a defender with a Markov process, where the defender can invest in three protection schemes, namely prevention (e.g., secure code development), detection (e.g., intrusion detection systems), and cyber insurance.

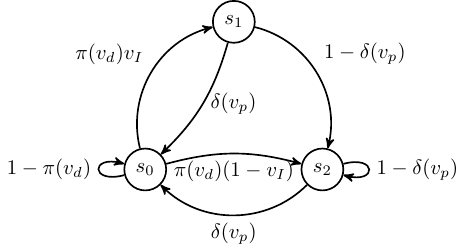
example markov process

Markov process that describes changes in the security of the system. The system has a vulnerable state S0 and two secure states S1 and S2, which differ in that S_1 occurs with insurance

Unlike other models, this project assumes that the defender cannot penalize the attackers, since in many cases the responsible of cyber crimes remains anonymous or cannot be prosecuted. I investigate the optimal strategies of both defender and attacker using stochastic dynamic programming. This research has contributed to understand the role of insurance to handle cyber risks. First, uncertainties in the actions of attackers make insurance more attractive. Moreover, insurance can improve the investment in either prevention or detection, when the premium is high or low, respectively. However, the defender needs incentives to purchase cyber insurance, but insurance alone doesn’t guarantee an adequate protection level. Concretely, policies with unlimited coverage can lead to perverse incentives that degrade the investments in security.

Selected publications

  1. C. Barreto, A. A. Cardenas, and A. Bensoussan, “Optimal security investments in a prevention and detection game”, in Proceedings of the hot topics in science of security: symposium and bootcamp, HoTSoS (2017), pp. 24–34.

  2. C. Barreto and A. A. Cardenas, “Optimal risk management in critical infrastructures against cyber-adversaries”, in 2017 ieee conference on control technology and applications (ccta) (Aug. 2017), pp. 2027–2032.